La compression

Synthèses

FORMONT Pierre
KACED Tarik
THIERY Jérémie

Bibliographie

Internet
Ecrits

Autres

Glossaire

LA COMPRESSION

INTRODUCTION

    En clair, la compression consiste à réduire la taille physique de l’information. C’est à dire que l’on va réduire l'emplacement requis sur un support de stockage.

     Pourquoi compresser alors qu'il suffirait d'augmenter la capacité des supports de stockage pour pouvoir contenir plus d'information. Pour une raison simple, le matériel a un prix et les capacités ont des limites. La plupart des logiciels de compression ne sont pas payants.

    Le volume d’information accessible aux utilisateurs d’Internet est en constante progression. La gestion de cette masse pose des problèmes de stockage de transport et d’accessibilité. En outre, la place disponible sur les machines n’est pas infinie et la capacité de la bande passante des réseaux est limitée.

    En conséquence, pour pallier ces problèmes, la compression devient alors intéressante. Dès 1940, de nombreux chercheurs ont mis au point des algorithmes différents basés sur la redondance des symboles dans les informations à traiter.
L’algorithme sert donc à optimiser les données grâce à leur structure de mise en forme.

    Il existe pour cela deux façons de compresser : avec pertes (ceux que nous étudierons) et sans pertes. Par la suite nous nous intéresserons uniquement aux algorithmes conservatifs. Les méthodes non conservatives sont utilisées pour des données bien précises (Audio, Vidéo, Images) dans le but de réduire leur taille jusqu'à la limite de la perception humaine.

    Parmi les algorithmes sans pertes, la plupart utilisent des dictionnaires qui dépendent de la méthode utilisée. Certains sont non-adaptatifs (statiques) il vont simplement attribuer un code plus court aux symboles les plus répétés. D’autres sont semi-adaptatifs ou adaptatifs (dynamiques) et construisent un dictionnaire au fur et à mesure de la redondance des données.

    Pour retrouver l’information initiale il suffit de décompresser. C’est le moment o il faut parfois réutiliser le dictionnaire pour restaurer avec intégrité l’information. Certains algorithmes utilisent la même méthode de compression et décompression elle se dit alors symétrique, sinon une des phases dure plus longtemps que l’autre c’est un codage asymétrique. Les algorithmes vont de ce fait être choisit en fonction de la nature des données à compresser.

  Exemple d'algorithme de compression :
  La compression RLE qui consiste à repérer les répétitions et à remplacer celles-ci par quelque chose de plus court :

Exemple : On veut compresser "bbbbbbbbbaaaaaccccccc".

On remarque que plusieurs caractères se répètent.
On remarque de même que l'on peut remplacer la chaîne par '9b5a7c' ce qui signifie littéralement :
neuf fois la lettre 'b', cinq fois la lettre 'a' et sept fois la lettre 'c'.
Voilà sur quoi repose un des algorithmes de compression.

CODAGE AFE

Le codage adaptatif des fréquences
ou
AFE (Adaptative Frequence Encoding)

1. Principe et méthode

        La méthode consiste à ajuster le codage des caractères en fonction de leur fréquence d’apparition dans le texte à compresser. Nous allons donc essayer d’attribuer un code plus court aux caractères les plus redondants.

        Tous les caractères sont généralement codés en ASCII sur 8 bits. L’idée, comme celle de Huffman, est de coder des éléments différemment sur moins de bits, de manière à gagner de la place.

        Lors de cette compression ils seront codés d’une façon particulière permettant de bien distinguer les caractères et surtout d’avoir désormais des codes allant de 4 à 11 bits.

Le « nouveau » code d’un caractère est décomposé en deux parties :

Un en-tête de 3 bits et un corps variant de 1 à 7 bits :

- L’en-tête détermine la taille du corps, c’est-à-dire le nombre de bits à lire après celui-ci pour reconstituer le code complet du caractère ( par exemple si il est « 111 », le corps est alors long de 7 bits car 111 en binaire est égal à 7 en base 10 ).

- Le corps du code représente le caractère codé.

Exemple d’un code : 100 0111

L’en-tête de l’exemple est « 100 », il aura donc un corps de 2^2 = 4 bits, qui vont suivre l’en tête.

Tous les caractères sont ainsi codés dans une table de transcription initiale ou dictionnaire.

A chacun est attribué une position et une fréquence ( initialement 0 ). Ils sont initialement rangés dans l’ordre de la table ASCII.

Code héxadécimal	Caractère	En-tête	Corps	Fréquence
00		000	0	0
01		000	1	0
02		001	0	0
03		001	1	0
04		010	00	0
05		010	01	0
06		010	10	0
07		010	11	0
08		011	000	0
09		011	001	0
0A		011	010	0
0B		011	011	0
0C		011	100	0
0D		011	101	0
0E		011	110	0
0F		011	111	0
10		100	0000	0
11		100	0001	0
12		100	0010	0
13		100	0011	0
14		100	0100	0
15		100	0101	0
16		100	0110	0
17		100	0111	0
18		100	1000	0
19		100	1001	0
1A		100	1010	0
1B		100	1011	0
1C		100	1100	0
1D		100	1101	0
1E		100	1110	0
1F		100	1111	0
20	espace	101	00000	0
21	!	101	00001	0
22	"	101	00010	0
23	#	101	00011	0
24	$	101	00100	0
25	%	101	00101	0
26	&	101	00110	0
27	'	101	00111	0
28	(	101	01000	0
29	)	101	01001	0
2A	*	101	01010	0
2B	+	101	01011	0
2C	,	101	01100	0
2D	-	101	01101	0
2E	.	101	01110	0
2F	/	101	01111	0
30	0	101	10000	0
31	1	101	10001	0
32	2	101	10010	0
33	3	101	10011	0
34	4	101	10100	0
35	5	101	10101	0
36	6	101	10110	0
37	7	101	10111	0
38	8	101	11000	0
39	9	101	11001	0
3A	:	101	11010	0
3B	;	101	11011	0
3C	<	101	11100	0
3D	=	101	11101	0
3E	>	101	11110	0
3F	?	101	11111	0
40	@	110	000000	0
41	A	110	000001	0
42	B	110	000010	0
43	C	110	000011	0
44	D	110	000100	0
45	E	110	000101	0
46	F	110	000110	0
47	G	110	000111	0
48	H	110	001000	0
49	I	110	001001	0
4A	J	110	001010	0
4B	K	110	001011	0
4C	L	110	001100	0
4D	M	110	001101	0
4E	N	110	001110	0
4F	O	110	001111	0
50	P	110	010000	0
51	Q	110	010001	0
52	R	110	010010	0
53	S	110	010011	0
54	T	110	010100	0
55	U	110	010101	0
56	V	110	010110	0
57	W	110	010111	0
58	X	110	011000	0
59	Y	110	011001	0
5A	Z	110	011010	0
5B	[	110	011011	0
5C	\	110	011100	0
5D	]	110	011101	0
5E	^	110	011110	0
5F	_	110	011111	0
60	`	110	100000	0
61	a	110	100001	0
62	b	110	100010	0
63	c	110	100011	0
64	d	110	100100	0
65	e	110	100101	0
66	f	110	100110	0
67	g	110	100111	0
68	h	110	101000	0
69	i	110	101001	0
6A	j	110	101010	0
6B	k	110	101011	0
6C	l	110	101100	0
6D	m	110	101101	0
6E	n	110	101110	0
6F	o	110	101111	0
70	p	110	110000	0
71	q	110	110001	0
72	r	110	110010	0
73	s	110	110011	0
74	t	110	110100	0
75	u	110	110101	0
76	v	110	110110	0
77	w	110	110111	0
78	x	110	111000	0
79	y	110	111001	0
7A	z	110	111010	0
7B	{	110	111011	0
7C	\|	110	111100	0
7D	}	110	111101	0
7E	~	110	111110	0
7F		110	111111	0
80	€	111	0000000	0
81		111	0000001	0
82	‚	111	0000010	0
83	ƒ	111	0000011	0
84	„	111	0000100	0
85	…	111	0000101	0
86	†	111	0000110	0
87	‡	111	0000111	0
88	ˆ	111	0001000	0
89	‰	111	0001001	0
8A	Š	111	0001010	0
8B	‹	111	0001011	0
8C	Œ	111	0001100	0
8D		111	0001101	0
8E	Ž	111	0001110	0
8F		111	0001111	0
90		111	0010000	0
91	‘	111	0010001	0
92	’	111	0010010	0
93	“	111	0010011	0
94	”	111	0010100	0
95	•	111	0010101	0
96	–	111	0010110	0
97	—	111	0010111	0
98	˜	111	0011000	0
99	™	111	0011001	0
9A	š	111	0011010	0
9B	›	111	0011011	0
9C	œ	111	0011100	0
9D		111	0011101	0
9E	ž	111	0011110	0
9F	Ÿ	111	0011111	0
A0		111	0100000	0
A1	¡	111	0100001	0
A2	¢	111	0100010	0
A3	£	111	0100011	0
A4	¤	111	0100100	0
A5	¥	111	0100101	0
A6	¦	111	0100110	0
A7	§	111	0100111	0
A8	¨	111	0101000	0
A9	©	111	0101001	0
AA	ª	111	0101010	0
AB	«	111	0101011	0
AC	¬	111	0101100	0
AD		111	0101101	0
AE	®	111	0101110	0
AF	&hibar;	111	0101111	0
B0	°	111	0110000	0
B1	±	111	0110001	0
B2	²	111	0110010	0
B3	³	111	0110011	0
B4	´	111	0110100	0
B5	µ	111	0110101	0
B6	¶	111	0110110	0
B7	·	111	0110111	0
B8	¸	111	0111000	0
B9	¹	111	0111001	0
BA	º	111	0111010	0
BB	»	111	0111011	0
BC	¼	111	0111100	0
BD	½	111	0111101	0
BE	¾	111	0111110	0
BF	¿	111	0111111	0
C0	À	111	1000000	0
C1	Á	111	1000001	0
C2	Â	111	1000010	0
C3	Ã	111	1000011	0
C4	Ä	111	1000100	0
C5	Å	111	1000101	0
C6	Æ	111	1000110	0
C7	Ç	111	1000111	0
C8	È	111	1001000	0
C9	É	111	1001001	0
CA	Ê	111	1001010	0
CB	Ë	111	1001011	0
CC	Ì	111	1001100	0
CD	Í	111	1001101	0
CE	Î	111	1001110	0
CF	Ï	111	1001111	0
D0	Ð	111	1010000	0
D1	Ñ	111	1010001	0
D2	Ò	111	1010010	0
D3	Ó	111	1010011	0
D4	Ô	111	1010100	0
D5	Õ	111	1010101	0
D6	Ö	111	1010110	0
D7	×	111	1010111	0
D8	Ø	111	1011000	0
D9	Ù	111	1011001	0
DA	Ú	111	1011010	0
DB	Û	111	1011011	0
DC	Ü	111	1011100	0
DD	Ý	111	1011101	0
DE	Þ	111	1011110	0
DF	ß	111	1011111	0
E0	à	111	1100000	0
E1	á	111	1100001	0
E2	â	111	1100010	0
E3	ã	111	1100011	0
E4	ä	111	1100100	0
E5	å	111	1100101	0
E6	æ	111	1100110	0
E7	ç	111	1100111	0
E8	è	111	1101000	0
E9	é	111	1101001	0
EA	ê	111	1101010	0
EB	ë	111	1101011	0
EC	ì	111	1101100	0
ED	í	111	1101101	0
EE	î	111	1101110	0
EF	ï	111	1101111	0
F0	ð	111	1110000	0
F1	ñ	111	1110001	0
F2	ò	111	1110010	0
F3	ó	111	1110011	0
F4	ô	111	1110100	0
F5	õ	111	1110101	0
F6	ö	111	1110110	0
F7	÷	111	1110111	0
F8	ø	111	1111000	0
F9	ù	111	1111001	0
FA	ú	111	1111010	0
FB	û	111	1111011	0
FC	ü	111	1111100	0
FD	ý	111	1111101	0
FE	þ	111	1111110	0
FF	ÿ	111	1111111	0

  Ce nouveau codage permet finalement le codage de la moitié des caractères sur moins de 8 bits ( 4 minimums ) mais d’autres seront en contrepartie codés sur plus de 8 bits … Le but de l'algorithme est maintenant d’attribuer les codes les plus courts aux caractères les plus fréquents, pour gagner de la place.

  Lors de la compression du texte, le compresseur va lire tous les éléments et les ranger dans le dictionnaire en fonction de leur fréquence et ce, au fur et à mesure de la lecture.

  La fréquence d’un caractère augmente alors de 1 à chaque fois qu’il est rencontré lors de la lecture, le caractère est reclassé dans la table en fonction de sa nouvelle fréquence. Il prend généralement la place d’un autre caractère et décale tous ceux situés en dessous d’un cran vers le bas. On dit que le dictionnaire est dynamique, il change en effet à chaque caractère lu.

  Les fréquences hautes se trouveront finalement au début de la table avec un code plus court.

        Le principe est simple, si les caractères les plus redondants sont codés sur 4 bits, ils prendront alors moins de place que s’ils étaient codés sur 8 bits ! ! Logiquement d’autres caractères devront être codés sur 8, 9, 10 ou 11 bits…mais ils sont beaucoup moins fréquents d’où un gain logique de place.

  On obtient finalement une table de référence avec les nouveaux codages de tous les caractères.

  L’ensemble du texte compressé comprendra une table de codage suivie de l’information.

Supposons que nous sommes en pleine compression et que l'on arrive au stade ci-dessous :

Caractère	en-tête	corps	fréquence
'A'	000	0	27
'Z'	000	1	27
...	...	...	...
'E'	100	1110	26
'C'	100	1111	5
'B'	101	00000	2

Si le prochain caractère lu est un 'E' : on ecrira '100 1110', sa fréquence sera de 27 et il se placera au tout début de la table :

Caractère	en-tête	corps	fréquence
'E'	000	0	27
'A'	000	1	27
'Z'	001	0	27
...	...	...	...
'C'	100	1111	5
'B'	101	00000	2

on remarquera que les caractères allant de l'ancienne position de 'E' à sa nouvelle position (du caractère 'A' inclu au caractère 'C' exclu) ont changé de code.

  Cette information est ensuite stockée sur un disque dur ou transmise à un autre PC. La décompression va permettre de la déchiffrer le jour où l’on aura besoin de la lire.

  La méthode est la même que pour la compression : la compression et la décompression sont symétriques. Pour qu’elle fonctionne bien, elle doit suivre le même parcours que la compression avec la même table de codage.

  Elle commence par la lecture des 3 premiers bits de l’information ( l’en tête ) qui permet de connaître le nombre de bits à lire pour reconstituer le code au complet d’un élément. Il faut ensuite utiliser la table de référence obtenue lors de la compression pour trouver le caractère attribué à ce code.

  Tous les bits de l’information vont être décodés ainsi de suite jusqu’à la fin…

  Le texte compressé sera finalement intégralement reconstitué, c’est une compression sans perte !

2. Problème

        Ce codage possède en fait deux inconvénients :

  L’information traitée peut posséder des caractères ayant des fréquences énormes ! Pour pallier ce problème, il suffit simplement de fixer un plafond ( souvent à 255, c’est-à-dire la valeur maximale d'un octet ), une fois le seuil de ce plafond dépassé, la fréquence du caractère est divisée par deux et on le reclasse dans la table…

  L’autre problème est que si un élément est très fréquent dans une partie de texte et inexistant par la suite, son codage sera « trop petit » par rapport à sa fréquence moyenne…il sera résolu de la même manière que le précédent.

3. Conclusion

Finalement, du point de vue compression, quel que soit l’élément, on le codera au mieux sur 4 bits ( au lieu de 8 ) donc on ne pourra gagner théoriquement et au plus de 50 % de la codification initiale. Mais en pratique, cet algorithme réalise une compression de moyenne de 5 à 20 %.

Cet inconvénient majeur fait que ce codage est quasi inutilisé.

télécharger le programme d'exemple du codage AFE

CODAGE HUFFMAN

1. Détails historiques :

David A. HUFFMAN en 1952 publie le résultat de ses recherches dans un article intitulé "A method for the construction of minimum redundancy codes" son algorithme qui permet de compresser les données sans perte. Son étude se fonde sur l'idée que certains caractères sont susceptibles d'apparaître plus souvent que d'autres dans un fichier, laissant la possibilité de les coder sur un nombre de bits plus restreint. Le codage HUFFMAN est désormais un standard en matière de compression. Créé à la base pour des fichiers de texte, cette méthode a su séduire les concepteurs et est désormais adaptée à tout types de fichiers. L'algorithme de HUFFMAN est une solution au problème de l'élaboration des codes comme il a été posé pour les algorithmes de codage statistique.

2. Le principe :

  La compression de HUFFMAN consiste à attribuer un nouveau code à chaque caractère. La taille de ce code va varier selon la fréquence d’apparition du caractère dans le fichier.

  Le codage de HUFFMAN est un codage entropique (probabilités d’apparition d’un caractère) qui a la propriété d'être optimal car il donne la plus petite moyenne de longueur de code de toutes les techniques de codage statistique.

  Pour compresser, il va falloir choisir comme unité de codage le bit; car les caractères sont codés sur un octet qui lui-même est constitué de 8 bits. Donc pour pouvoir compresser, on devra pouvoir coder les caractères sur moins de 8 bits. D’où l’unité choisie.

  Pour que la compression soit efficace on se propose de recoder les caractères qui ont une occurrence très faible avec un grand nombre de bits et les caractères très fréquents seront codés sur une longueur binaire très courte (moins de 8 bits). En effet, certains caractères n’apparaissant que peu de fois auront un code plus long que la normale (8 bits) ce qui n’empêche pas la compression car ces caractères à « codes longs » (fréquence d’apparition basse) représentent par définition une petite partie du fichier, tandis que les caractères qui se verront attribuer un « code court » représentent eux une plus grande partie du fichier car leur fréquence d’apparition est forte. Ce qui signifie bien que cet algorithme soit basé sur la redondance des caractères dans un fichier, c’est à dire que le fait que certains caractères se répètent plus de fois que d’autres.

  Il va de soi que le code de chaque caractère doit être unique. Mais il faut de plus qu’un code ne soit pas le début d’un autre sinon il serait impossible de savoir à quel caractère appartient ce code. C’est pour cela que le codage de HUFFMAN est « instantané », ce qui signifie qu'aucun code n'est le préfixe d'un autre. Cette propriété s'assure de l'unicité de décodage de chaque code. Par exemple : il ne peut avoir les codes ‘100’ et ‘1001’ en même temps, sinon dans ce cas faudra t-il décoder ‘100’ puis ‘1’ ou ‘1001’. Sans cette propriété le système de codage ne serait pas fonctionnel.

  Toutes ces caractéristiques du codage de HUFFMAN montrent qu’il faudra utiliser un système basé sur une structure arborescente appelée « arbres binaires ».

3. La méthode :

Compression des données:

Pour mieux comprendre l’algorithme nous allons utiliser un exemple. Nous allons compresser le fichier suivant. Il s’agit d’un texte composé d’un alphabet de 6 lettres : A, B, C, D, E et F.

AABBCCCCCDDDEEEEEEEF

Il y a 20 caractères en tout

Première phase : élaboration des codes de HUFFMAN.

Cette phase consiste à générer les futurs codes attribués aux caractères présents dans le fichier à partir de la lecture du fichier. C’est à partir de ces codes que le système de codage sera basé. Pour créer ces codes il faudra construire un arbre binaire dont les noeuds seront les caractères et la valeur de ces noeuds sera la fréquence d’apparition.

Pour construire l’arbre binaire, on effectue des réductions successives jusqu'à la fin de la table. Cela consiste à prendre les deux éléments de la table ayant les plus petites fréquences qui seront des feuilles de l’arbre et à les assembler pour former un nouvel élément qui sera un nœud de l’arbre. Cet élément aura pour fréquence la somme des deux fréquences des éléments que l’on vient d’associer et ceux-ci sont supprimés de la table. La table est ensuite retriée, et ainsi de suite jusqu'à ce qu’il ne reste qu’un seul élément appelé racine.

Cette partie de l’algorithme se compose des étapes suivantes :

1. Faire la liste des caractères présents et les trier par probabilité décroissante; ces caractères constituent les nœuds d'origine de l'arbre de HUFFMAN.

Il y a d’abord lecture des caractères un par un. On construit en parallèle une table d'occurrence pour chaque caractère. Ici, le premier caractère lu est un " A ", on ajoute l’élément ‘A’ à la table et son occurrence devient 1. Lorsqu’on relira ‘A’ son occurrence sera incrémentée de 1. Il faut faire cela avec tous les caractères du fichier jusqu’à la fin. A la fin de la lecture du fichier, on obtient une table qui nous indique combien de fois un caractère du fichier est répété.
Il faut en suite bien sûr réorganiser cette table afin qu'elle soit utilisable. Il suffit de la trier dans l'ordre décroissant des probabilités.

Lettre	Occurrence	Probabilité
F	1	0,05
A	2	0,1
B	2	0,1
D	3	0,15
C	5	0,25
E	7	0,35

2.Prendre les deux nœuds de plus faible probabilité, les fusionner en un nœud dont la probabilité est égale à la somme de leur probabilité.

Ici on construit un nœud avec les deux éléments de plus faible fréquence. Le plus petit sur la branche de droite (appelée feuille droite), l'autre sur la branche de gauche (appelée feuille gauche).

3. Répéter l'étape 2 jusqu'à ce qu'il ne reste qu'un seul nœud (de probabilité 1) qui devient la racine de l'arbre binaire ainsi constitué.

A partir de la table des noeuds, on opère donc par réductions successives.

F et A ont les plus petites fréquences, on les fusionne en un noeud dont la valeur est la somme des fréquences F et A

La table est retriée et on opère une seconde fois avec les deux noeuds de plus basse fréquence

L'arbre final est ainsi constitué et la suite de l'algorithme va consister à tirer de celui les codes tant attendus.

4. Récupérer les nouveaux codes grâce à l’arbre binaire créé.

Il ne reste plus qu’à attribuer un code pour chaque feuille. Pour ce faire, on utilise une méthode très simple. On commence à la racine, à chaque fois que l’on se déplace vers la droite on attribue le code ‘1’ à l’élément sur lequel on se trouve (feuille ou nœud), à chaque pas vers la gauche on attribue le code ‘0’ à l’élément sur lequel on se trouve (feuille ou nœud). Remarque : on peut tout aussi bien inverser ce code si bien qu’à une branche droite le code pourrait être ‘0’ et à une branche gauche ‘1’. Ceci est sans importance. Maintenant il ne reste plus qu’à lire chaque octet et à écrire son code équivalent.

Deuxième phase : l’encodage.

Après lecture des codes de l’arbre binaire de HUFFMAN on a :

Caractère	Code attribué
A	0000
B	001
C	01
D	11
E	10
F	0001

Il ne reste plus qu’à relire une nouvelle fois chaque caractère du fichier un par un et d’écrire dans le fichier compressé le code attribué au caractère que l’on vient de relire.

Ici on obtient donc :

0000 0000 001 001 01 01 01 01 01 11 11 11 10 10 10 10 10 10 10 0001

Comme l'unité est le bit, il faut regrouper les codes par huit pour connaître le nombre de caractères. Ce qui fait en tout : 48 bits soit 6 octets donc 6 caractères au lieu de 20.

C'est à dire que ce fichier a été compressé à (20-6)/20 = 70%.
Il occupe donc (1 - (20/6)/20) = 30% de l'espace stockage initial.
Soit un taux de compression de 20/6 = 3,3

Bien sur, il faudra inclure le dictionnaire, c’est à dire chaque caractère et son code, au fichier pour pouvoir décompresser les données. Ce qui réduira le taux de compression.

Décompression des données

Pour décompresser c’est très simple. Il faut :

1. Lire l’en-tête du fichier (début du fichier), c’est le dictionnaire. On obtient alors les caractères et leur code. On lit donc :

Caractère	Code attribué
A	0000
B	001
C	01
D	11
E	10
F	0001

2. Reconstruire l’arbre.

Grâce à l’étape 1, nous sommes désormais capables de reconstituer l’arbre binaire tel qu’il était en phase de compression. En effet, nous disposons des codes de chaque caractère, donc on créé la racine et on lit le code de chaque caractère bit à bit pour refaire l’arbre (par exemple : si c’est un ‘1’ il faudra un fils droit (un nœud à droite de la racine) et à la fin de la lecture du code le dernier nœud sera donc une feuille de l’arbre et aura pour valeur : le caractère).

Caractère	Code attribué	Déplacement dans l'arbre
A	0000	Droite, Droite, Droite, Droite
B	001	Droite, Droite, Gauche
C	01	Droite, Gauche
D	11	Gauche, Gauche
E	10	Gauche, Droite
F	0001	Droite, Droite, Droite, Gauche

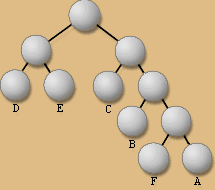
3. Décoder le fichier.

Maintenant, il ne reste plus qu’à lire le reste du fichier bit par bit et de se déplacer selon la méthode évoquée précédemment. La direction prise à chaque noeud est en fonction de la valeur du bit lu, et ce jusqu'à une feuille comportant la valeur décompressée (si on lit un ‘0’ il faudra avancer d’un pas vers la gauche). Dès que l’on arrive à une feuille, on s’arrête puis on écrit le caractère correspondant à la valeur de la feuille, on revient à la racine et on continue la lecture ainsi de suite jusqu’à la fin du fichier.

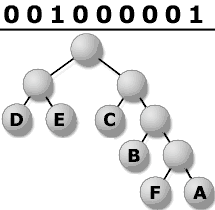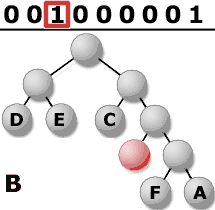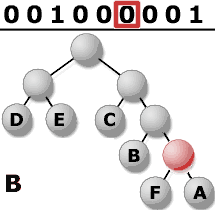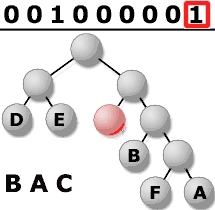
4. Explications complémentaires :

1. La probabilité d’apparition d’un caractère ou fréquence d’apparition est définie par son nombre d’occurrence dans le fichier divisé par le nombre total de caractère dans le fichier. Elle peut aussi x’exprimer en pourcentage. Claude SHANON (qui à lui aussi son propre algorithme de compression assez similaire de celui de HUFFMAN) à exposé sa théorie de l’information (un message contient une quantité finie d’information, un fichier image par exemple contient une information qui n’est pas minimale, on peut la réduire mais pas au-delà de son expression minimale), et par exemple une formule mathématique précise appelée l’entropie (notée E) qui s’exprime en bit/caractères qui permet de calculer par exemple la quantité d’information minimale dont un message (fichier) peut être réduit.

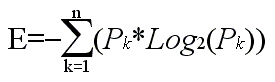
(ou n est le nombre de caractères et Pk la probabilité de du caractère k)

Lettre	Probabilité (Pk)	*PkLog2(Pk)**
F	0,05	-0,216
A	0,1	-0,332
B	0,1	-0,332
D	0,15	-0,410
C	0,25	-0,500
E	0,35	-0,530
Entropie		2,321

L'entropie est donc de 2,321 bits/caractères soit 2,321*20 = 46,42 bits en tout. L'unité étant le bit on ne peut accepter les nombres à virgules. Cela fait donc 47 bits, l'algorithme de HUFFMAN nous donne lui 48 bits. Cette légère erreur est due à l'unité qui est le bit. Cependant l'algorithme de HUFFMAN est bien optimal selon la théorie de l'information.

2.Il y a en fait trois grandes nuances de l'algorithme, qui se caractérisent par une création de l’arbre différente:

- La méthode HUFFMAN non adaptative: l'arbre est construit à partir d'une table des fréquences fixe (constante), non établie à partir des données à traiter. On dit que le compresseur est adapté à un type de données spécifique. Cette méthode est peu utilisée. Exemple fichiers texte d’une langue précise.

Exemple de dictionnaire statique :

Lettre	Français	Anglais
A	0.1732	0.1859
B	0.0690	0.0642
C	0.0068	0.0127
D	0.0339	0.0317
E	0.1428	0.1031
F	0.0095	0.0208
G	0.0098	0.0152
H	0.0048	0.0467
I	0.0614	0.0575
J	0.0024	0.0008
K	0.0006	0.0049
L	0.0467	0.0321
M	0.0222	0.0198
N	0.0650	0.0574
O	0.0464	0.0632
P	0.0261	0.0152
Q	0.0104	0.0008
R	0.0572	0.0484
S	0.0624	0.0514
T	0.0580	0.0796
U	0.0461	0.0228
V	0.0104	0.0083
W	0.0005	0.0175
X	0.0035	0.0013
Y	0.0018	0.0164
Z	0.0006	0.0005

- La méthode HUFFMAN semi-adaptative (parfois appelée non adaptative), c’est la méthode expliquée ici. La table des fréquences est établie à partir de la lecture des données à compresser.

- La méthode HUFFMAN adaptative: la table des fréquences est construite au fur à mesure de la compression (comme pour l’algorithme LZW), l'arbre est donc en perpétuelle évolution au cours de la compression.

L’avantage de cette méthode est qu’il n’est pas nécessaire de transmettre le dictionnaire ainsi créé. La compression commence avec un arbre initial (non adapté aux données). De plus, cette méthode se contente de lire d’une traite les données et de les compresser en même temps et non de lire deux fois les données et donc de pouvoir être incorporée dans des modems par exemple.

5. Le bilan :

C’est un algorithme statistique semi-adaptatif, asymétrique sans pertes, avec dictionnaire statique :

La phase de compression et de décompression ne sont pas identiques c’est donc une compression asymétrique.

La totalité des données est restituée à la décompression c’est donc un algorithme sans pertes.

L’algorithme se sert de la fréquence d’apparition de chaque caractère pour l’encodage c’est donc un algorithme statistique.

L’algorithme génère des codes suivant la fréquence d’apparition des caractères dans tout le fichier c’est donc un algorithme semi-adaptatif.

Un dictionnaire est créé et l’algorithme utilisé pour la compression est semi-adaptatif ou non-adaptatif ce dictionnaire est donc statique.

Pour pouvoir compresser, il faut lire deux fois le fichier en entier donc on perd un temps précieux qui empêche par exemple l’emploi de cette méthode semi-adaptative dans les modems ou dans les fax.

Dans ce type de compression, le décompresseur doit avoir les informations qui lui permettent de décompresser. C'est-à-dire que l'on devra faire figurer en tête de fichier les clés de décodage des caractères (dictionnaire). Pour les petits fichiers, l’espace accaparé par le dictionnaire peut être proportionnellement trop grand et risque d’induire un gain négatif c’est à dire une compression qui fait l’inverse de compresser!

Pour pallier ce problème, il existe des tables de statistiques constantes intégrées au compresseur si l’on veut compresser du texte par exemple. On utilisera une table de l'alphabet lexical. Ces probabilités d'apparition changent suivant la langue utilisée dans le fichier source. Comme c’est une constante, on n’a pas besoin de la transmettre.

Malgré tous ces défauts et son ancienneté, cet algorithme est un des plus utilisés dans la compression de données car le taux de compression est souvent élevé en moyenne de 45 à 60% et la décompression est rapide.

CODAGE LZW

1. Origine et principe de base

        La méthode LZW (pour Lempel-Ziv-Welch) est dérivée de la méthode LZ, du nom de ses créateurs Lempel et Ziv. Cette méthode est utilisable par n'importe qui, contrairement à la méthode LZW, qui est protégée par des copyrights internationaux. Néanmoins, le principe de base reste le même et c'est celui-ci que nous allons expliquer.

        Le principe de compression est basé sur la création d'un dictionnaire dynamique, créé à chaque phase de compression ou de décompression, afin de ne pas avoir à le stocker. Ce dictionnaire est un dictionnaire de chaînes de caractères. Le principe repose sur le fait qu'une chaîne de caractères peut apparaître plusieurs fois dans un même fichier, et on exploite ce phénomène en stockant ces chaînes dans la table ASCII au même titre qu'un seul caractère des rangs 0 à 255 de la table ASCII. Pour cela, on agrandit la table ASCII, en la dotant des rangs 256 et 257, respectivement nommés "code latent" et "code lu". Les chaînes ne seront donc stockées qu'à partir du rang 258. Examinons maintenant comment se présente la phase de compression.

2. Compression

        Nous allons voir comment la phrase "AIDE TOI LE CIEL T AIDERA" est compressée. L'algorithme regarde donc le premier caractère "A" et le place au niveau du code latent. Puis on examine le deuxième caractère I", et on regarde si la chaîne "code latent + code lu", c'est à dire "AI" existe dans le dictionnaire :

        Comme le dictionnaire est seulement composé de la table ASCII, cette chaîne n'existe pas. Elle est donc stockée dans la table au rang 258. Puis on émet le rang du code latent ("A"). Le code lu "I" devient alors code latent. On lit ensuite le troisième caractère, qui est "D" :

        La chaîne "code latent + code lu" ("ID") est donc ajoutée au dictionnaire au rang 259, puis on émet le rang du code latent "I", et le code lu "D" devient code latent.

  On lit ensuite le 4ème caractère "E" :

  Et on crée la chaîne "DE" au rang 260, l'algorithme émet le rang du code latent "D", et le code lu "E" devient code latent.

  Le processus est répété à l'identique jusqu'à tomber sur une chaîne du dictionnaire déjà existante (en réalité créée quelques instants plus tôt). Par exemple, la chaîne "E espace" existe déjà dans le dictionnaire.

        A ce moment-là, l'algorithme examine le prochain caractère et regarde si la chaîne "E espace C" existe dans le dictionnaire. Comme cette recherche échoue, cette chaîne est ajoutée au dictionnaire à un nouveau rang, et on a créé ainsi une chaîne de 3 caractères. Puis la lecture de la phrase et sa compression se déroulent comme le montre la figure 1.

Etape	Code latent	Code lu	Emis	Chaîne stockée	Indice de la chaîne
1	A	I	A = 65	AI	258
2	I	D	I = 73	ID	259
3	D	E	D = 68	DE	260
4	E	espace	E = 69	E espace	261
5	espace	T	espace = 32	espace T	262
6	T	O	T = 84	TO	263
7	O	I	O = 79	OI	264
8	I	espace	I = 73	I espace	265
9	espace	L	espace = 32	espace L	266
10	L	E	L = 76	LE	267
11	E	espace	SP	rien	aucun
12	E espace	C	E espace = 261	E espace C	268
13	C	I	C = 67	CI	269
14	I	E	I = 73	IE	270
15	E	L	E = 69	EL	271
16	L	espace	L = 76	L espace	272
17	espace	T	rien	rien	aucun
18	espace T	espace	espace T = 262	espace T espace 273
19	espace	A	espace = 32	espace A	274
20	A	I	rien	rien	aucun
21	AI	D	AI = 258	AID	275
22	D	E	rien	rien	aucun
23	DE	R	DE = 260	DER	276
24	R	A	R = 82	AR	277
25	A		A = 65

Figure 1

        Le code est aussi stocké sous forme binaire et pas seulement sous la forme des rangs du dictionnaire. Il est initialement stocké sur 8 bits mais a l'étape 11, on rencontre le code SP. Il s'agit d'un repère annonçant que dorénavant, l'émission des adresses se fera sur 9 bits au lieu de 8, afin de pouvoir gérer des adresses de tailles variables. Ce repère n'est d'aucune utilité pour l'algorithme de compression, mais il est très important pour l'algorithme de décompression et ceci est une des particularités du système LZW : les deux algorithmes communiquent, s'échangeant mutuellement des informations. Ce système de communication entre les deux phases de l'algorithme est extrêmement utile et à donc été à l'origine d'un grand nombre de variantes, comme la compression LZO (Lempel-Ziv-Oberhumer). On peut voir un résumé du dictionnaire dans la figure 1 : ce tableau présente toutes les chaînes de caractères créées par l'algorithme et leur rang dans le dictionnaire. Une fois que le fichier a été compressé, il faut que l'on puisse le décompresser. Passons donc à la phase de décompression.

3. Décompression

        Pour la phase de décompression, le dictionnaire est recréé sur place, ce qui évite d'avoir à le transmettre, ce qui prendrait de la place et baisserait ainsi l'efficacité de l'algorithme. Ainsi le dictionnaire est composé de la table ASCII, comme pour la compression, et des codes 256 et 257, correspondant respectivement aux "code latent" et "code reçu". On se rappelle que l'algorithme de compression émettait les rangs des codes latents. L'algorithme de décompression reçoit donc ces indices dans l'ordre où ils ont été émis. Le premier indice est reçu, il correspond au "A" et est placé dans le code latent. L'algorithme regarde si la chaîne "code latent+code reçu" existe dans le dictionnaire : le code latent étant initialement vide, la recherche est fructueuse et on restitue le premier caractère, avant de le placer en code latent :

        Ensuite un deuxième indice est reçu, celui du "I" : il est placé en code reçu et la recherche de la chaîne "code latent+code reçu" dans le dictionnaire ne permet pas de trouver la chaîne "AI". Celle-ci est donc ajoutée dans le dictionnaire au rang 258, puis on restitue le deuxième caractère "I" et on le place en code latent.

  Le troisième caractère, "D", est ensuite réceptionné et placé en code reçu : on crée la chaîne "ID" dans le dictionnaire au rang 259 car elle ne s'y trouve pas, puis on restitue le "D" et on le place en code latent.

  Tout le texte est ainsi recréé lettre par lettre, jusqu'à ce qu'on trouve une chaîne déjà existante dans le dictionnaire. Par exemple la chaîne "E espace" a été créée à la 5ème étape et on la retrouve à la 12ème étape : à ce moment-là, on restitue la chaîne "E espace" dans le texte, et on crée une nouvelle chaîne constituée de "E espace C" dans le dictionnaire, car "E espace" est passé code latent.

Et toute la phrase est ainsi restituée d'un bout à l'autre, sans altérations.

Etape	Code latent	Code reçu	Rang du code reçu	Chaîne créée	Texte retranscrit
1	A	65	A
2	A	I	73	AI	AI
3	I	D	68	ID	AID
4	D	E	69	DE	AIDE
5	E	espace	32	E espace	AIDE
6	espace	T	84	espace T	AIDE T
7	T	O	79	TO	AIDE TO
8	O	I	73	OI	AIDE TOI
9	I	espace	32	I espace	AIDE TOI
10	espace	L	76	espace L	AIDE TOI L
11	L	E espace	261	LE	AIDE TOI LE
12	E espace	C	67	E espace C	AIDE TOI LE C
13	C	I	73	CI	AIDE TOI LE CI
15	I	E	69	IE	AIDE TOI LE CIE
16	E	L	76	EL	AIDE TOI LE CIEL
17	L	espace T	262	L espace	AIDE TOI LE CIEL
18	espace T	espace	32	espace T espace	AIDE TOI LE CIEL T
19	espace	AI	258	espace AI	AIDE TOI LE CIEL T AI
20	AI	DE	260	AID	AIDE TOI LE CIEL T AID
21	DE	R	82	DER	AIDE TOI LE CIEL T AIDER
22	R	A	65	RA	AIDE TOI LE CIEL T AIDERA

figure 2.

4. Conclusion :

Ainsi, pendant la phase de compression, un dictionnaire a été formé, puis, comme le fichier dans le même ordre qu'il a été lu, le dictionnaire a été recréé pendant la décompression. On évite comme cela d'avoir à envoyer le dictionnaire, donc on a un gain de temps, et de plus, le fichier est compressé, donc un gain de temps encore plus grand. L'avantage de cette méthode est qu'elle permet de faire des chaînes très longues codées sur très peu de place. De plus, les taux de compression sont assez élevés, de l'ordre de 45 à 55% en moyenne. Malheureusement, il faut, pour obtenir un véritable gain, des fichiers assez grands, supérieurs à un Mo, et qui sont susceptibles de présenter beaucoup de répétitions.

CONCLUSION

  L’importance de la compression est surtout due aux besoins qu’expriment les utilisateurs (transfert de quantités d’informations toujours plus importantes dans les délais les plus brefs ) les possibilités matérielles (divers canaux de transmission, capacité des mémoires) étant toujours limitées. Lorsque cela ne pose pas vraiment de problème, la compression permet de toute façon de faire des économies.

  Les méthodes de compression assez complexes que nous avons essayé de vous expliquer, comme HUFFMAN et LZW, sont efficaces et sophistiquées donc couramment utilisées (Ce qui n’est pas le cas de la compression AFE)

  Principaux atouts de l’utilisation de la compression de données :

  Gain en espace de stockage
    - L’espace disque requis est moindre
    - L’espace en mémoire requis est moindre

  Gain en temps sur les lectures / écritures
    - Moins de données à lire où à écrire physiquement sur disque
    - Compresser et écrire des données est plus rapide qu’écrire des données non-compressées
    - Décompresser et lire des données est plus rapide que lire des données non-compressées

  Gain sur les temps de transmission
    - Compresser des données puis les transmettre prend moins de temps que de transmettre des données non-compressées
    - Recevoir des données puis les décompresser prend moins de temps que de recevoir des données non-compressées

Les méthodes de compression permettent donc un gain de temps considérable.

Efficacité des différents algorithmes :

(1) : petit fichier
(2) : gros fichier

Test des différent logiciel de compression de données

Taux de compression(bleu) + vitesse(rouge)	Format	Logiciel
	ZIP	Winrar 2.8
	ACE	WinAce 1.31
	ZIP	Power Archiver 6.11.0
	RAR	WinRar 2.8
	ZIP	WinAce 2.02
	ZIP	WinZip 8
	ACE	WinAce 2.02
	RAR	WinRar 2.71
	LHA	Power Archiver 6.11.0
	CAB	WinAce 2.02
	BH	Power Archiver 6.11.0
	CAB	Power Archiver 6.11.0
selon www.cmetge.dixinet.com